Trapped Particles

Inverse problems in imaging of trapped particles

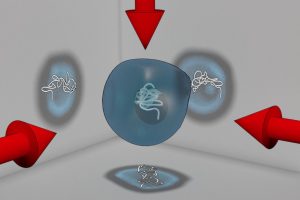
Optical tomographic (OPT) imaging provides quantitative three-dimensional (3D) information, the distribution of the refractive index of an optically translucent sample. However, for collecting the tomographic images one typically has to immobilize the sample and to rotate the entire probe, or the entire imaging system. An alternative approach dispenses with sample fixation and instead utilizes optical trapping to hold and move the sample in a contact-free manner. To specifically address the problematic issues with large objects we have recently developed a hybrid acoustic-optical trap which combines the benefit of the large trapping forces achievable by ultrasound waves with the real-time programmability of optical tweezers. The present subproject tackles some challenges that arise for tomographic imaging in a trap, especially for irregular shapes.

Computational Algorithms and Regularization Methods

We consider the imaging of a trapped cell with OPT. The cell is stably held or moved with programmable optical tweezers and is illuminated by a paraxial beam.  The most detailed mathematical model, for describing the light propagation, is based on Maxwell’s equations. However, the orientation of the specimen is uncertain and that makes the modeling of the measurement data much more complicated. Thus, standard back-projection formulas result in jittered and blurred 3D reconstructions. We will explore different ideas for de-jittering, taking an inverse problems point of view and a filtering approach.

Research Team

From Subproject: Quantitative Coupled Physics Imaging

Peter ElbauPrincipal Investigator

Denise SchmutzPhD student

From Subproject: Imaging of Trapped Particles

Monika Ritsch-MarteProfessor for Medical Physics Director of the Division for Biomedical Optics

Mia Kvåle LøvmoPhD student

From Subproject: Tomography with Uncertainties

Otmar ScherzerPrincipal Investigator Professor at the Faculty of Mathematics Computational Science Center

From Subproject: Motion Detection in Tomography and Microscopy

Gabriele SteidlPrincipal Investigator Professor at Technische Universität Berlin

Michael QuellmalzPostdoctoral Researcher