Inverse problems in imaging of trapped particles
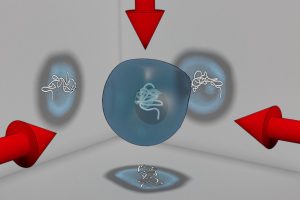
Optical tomographic (OPT) imaging provides quantitative three-dimensional (3D) information, the distribution of the refractive index of an optically translucent sample. However, for collecting the tomographic images one typically has to immobilize the sample and to rotate the entire probe, or the entire imaging system. An alternative approach dispenses with sample fixation and instead utilizes optical trapping to hold and move the sample in a contact-free manner. To specifically address the problematic issues with large objects we have recently developed a hybrid acoustic-optical trap which combines the benefit of the large trapping forces achievable by ultrasound waves with the real-time programmability of optical tweezers. The present subproject tackles some challenges that arise for tomographic imaging in a trap, especially for irregular shapes.
Computational Algorithms and Regularization Methods
We consider the imaging of a trapped cell with OPT. The cell is stably held or moved with programmable optical tweezers and is illuminated by a paraxial beam. The most detailed mathematical model, for describing the light propagation, is based on Maxwell’s equations. However, the orientation of the specimen is uncertain and that makes the modeling of the measurement data much more complicated. Thus, standard back-projection formulas result in jittered and blurred 3D reconstructions. We will explore different ideas for de-jittering, taking an inverse problems point of view and a filtering approach.
Research Team
From Subproject: Quantitative Coupled Physics Imaging
 Peter Elbau
Principal Investigator
Peter Elbau
Principal Investigator
 Denise Schmutz
PhD student
Denise Schmutz
PhD student
From Subproject: Imaging of Trapped Particles
 Monika Ritsch-Marte
Professor for Medical Physics
Monika Ritsch-Marte
Professor for Medical PhysicsDirector of the Division for Biomedical Optics
 Mia Kvåle Løvmo
PhD student
Mia Kvåle Løvmo
PhD student
From Subproject: Tomography with Uncertainties
 Otmar Scherzer
Principal Investigator
Otmar Scherzer
Principal InvestigatorProfessor at the Faculty of Mathematics
Computational Science Center
From Subproject: Motion Detection in Tomography and Microscopy
Institute of Mathematics
Strasse des 17. Juni 136
10587 Berlin
 Gabriele Steidl
Principal Investigator
Gabriele Steidl
Principal InvestigatorProfessor at Technische Universität Berlin
 Michael Quellmalz
Postdoctoral Researcher
Michael Quellmalz
Postdoctoral Researcher